Data Fit to 2-D Gaussian Function
Development of the wireless optical system KORUZA requires analysis of the IR optical beam to determine its divergence and calibrate a visible optical beam to be parallel with the invisible IR one. Optical power distribution follows the Gaussian distribution and with a measurement tool we can either obtain a small number of values simultaneously with multiple detectors or use a single detector and manually scan it across the beam. To measure the diameter and other properties a fit of experimental values to a Gaussian distribution is required. Since the GNU Octave software only support 1D fits, we have implemented a 2D fit function.
Once we have obtained a sufficient sample of measurement values, most of the computational softwares can construct a quite accurate fit in the case of one dimensional data. However, if data is more dimensional there are just few pre-build functions available. While Matlab offers a pre-build function ‘fittype’, which enables curve and surface fitting to a custom or predefined model, freely available Octave currently does not have a similar option.
We are introducing a possible approach to construct a Gaussian fit for 2-D data in the case where only a small set of measurements is known, using only basic arithmetic and logarithmic properties. Consequently, constructed solution is not limited to Octave and can be implemented in most computational software and programming language. Full details and mathematical derivation are presented in the note Data Fit to 2-D Gaussian Function. Octave code can be found on IRNAS GitHub.
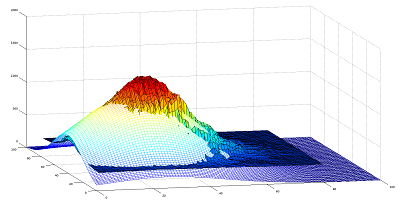
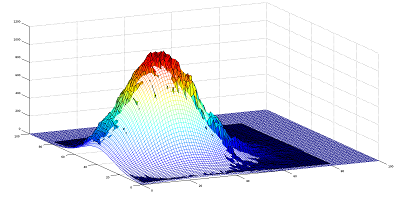
Based on the size of measurement sample and distribution on measurement points, we should not expect a very accurate fit, more an approximate model that can provide us with more information about the data. Below we can see Gaussian fit to the power measurement of the Gaussian laser beam, constructed on 9 measurements points, one in the centre, other 8 in two concentric circles, located on the 100x100 mm grid. Left plot represents constructed fit, using generic algorithm and the plot on the right fit after certain pre-known features of our data were taken into the account. Fit is not very accurate, however still useful for approximately locating the centre of the beam and determining its diameter (set appropriate threshold), which was the main objective.